Non-Contiguous Pattern Avoidance in Binary Trees
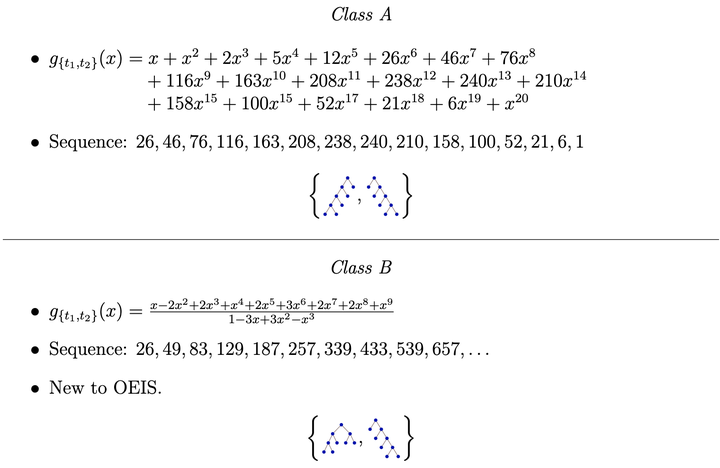 Two sequences generated from avoiding 5-leaf trees.
Two sequences generated from avoiding 5-leaf trees.
Abstract
In this paper we consider the enumeration of binary trees avoiding non-contiguous binary tree patterns. We begin by computing closed formulas for the number of trees avoiding a single binary tree pattern with 4 or fewer leaves and compare these results to analogous work for contiguous tree patterns. Next, we give an explicit generating function that counts binary trees avoiding a single non-contiguous tree pattern according to number of leaves and show that there is exactly one Wilf class of $k$-leaf tree patterns for any positive integer $k$. In addition, we give a bijection between between certain sets of pattern-avoiding trees and sets of pattern-avoiding permutations. Finally, we enumerate binary trees that simultaneously avoid more than one tree pattern.